통계학의 본질탐구(1) communication, Myth & Truth, Inspiration, necessity
Why Statistics?
우리가 일상생활에서 많이 보는 '숫자'에는 어떤 것이 있을까요? 특히 뉴스에서 자주 등장하는 숫자들로 살펴보겠습니다.
1. 경기도 수원시의 날씨

보아하니 24일 오전 9시에는 체감온도가 영하 24도까지 내려가는군요. 한파영향이 '경고'인 것을 보니 매우 추운 겨울인가 봅니다. 집에서 침대에 누워 넷플릭스를 보는 하루를 보내야겠군요. 외출하시는 분들은 롱패딩과 목도리를 갖춰 입고 따뜻하게 체온을 유지해야 하겠습니다.
2. 미국 중간선거(2022.11.08.)

미국은 6년마다 주마다 2명씩 총 100명의 상원(Senate)의원을 선출합니다. 대의민주주의를 바탕으로 주별 인구에 비례하여 2년마다 의원을 구성하는 하원(House of Representative)과 달리, 연방제를 바탕으로 모든 주가 동등한 위치에서 외교, 국방 등 국가의 중대한 사안을 논하기 위해 50개 주가 똑같은 인원으로 상원에 진출하는 제도가 구축된 것입니다.
선거를 치르지 않은 주를 포함하여 상원에서 민주당은 51석, 공화당은 49석을 확보하여 민주당이 신승(辛勝)을 거두었군요. 언론은 바이든 정부가 아슬아슬하게 겨우 이겼지만 국정운영이 여전히 쉽지 않을 것이라고 전망하기도 했고, 생각보다 공화당이 부진하여 여당을 견제할 절호의 기회를 놓쳤다고 평가하기도 했습니다. 우리나라에는 어떠한 영향을 미쳤을까요?
3. 삼성전자의 주가
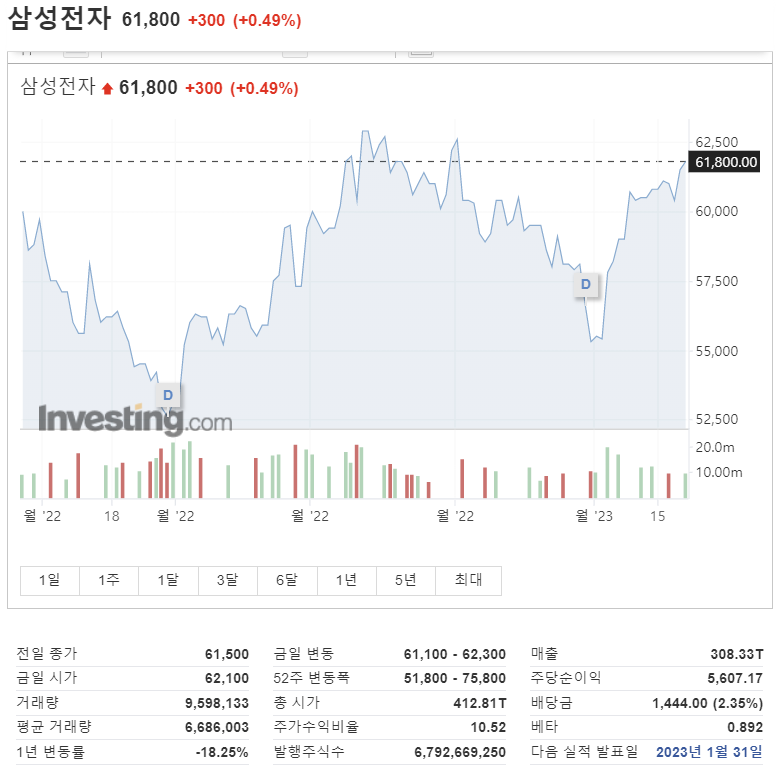
2023년 1월 23일 기준 삼성전자의 주가가 어떻게 흘러왔는지 보여주는군요. 2022년 9월 29일경에는 주가 5만 원대 초반까지 떨어졌다가 다시 평소 주가대로 회복했습니다. 1년 변동률이 -18.25%인 것을 보니 마음고생을 하셨을 분들이 꽤 많았을 것 같습니다. 다음 실적 발표일이 2023년 1월 31일이니, 신년 들어 어느 정도의 실적을 냈는지 챙겨볼 필요가 있겠군요.
자, 위의 3가지 '숫자들'의 공통점은 무엇일까요?

바로 "측정-정제-표현"의 과정을 거친 자료라는 점입니다.
1번 기상예보의 경우, 일별 평년기온을 측정해둔 자료와 기상청 내부의 시스템을 바탕으로 향후 3일 동안의 기온, 강수량 등을 시간 단위로 예측하여 시각화한 자료입니다. 2번 선거결과의 경우, 선거가 끝난 후 각 주에서 개표하여 어떤 후보가 이겼는지 판단하고 이긴 후보의 소속을 파악해서 어느 주에서 어떤 당이 이겼는지 시각화한 자료입니다. 그리고 3번 주식가격의 경우, 지난 몇 개월간 시가와 종가를 측정하고 실시간 거래가격을 추적하여 선 그래프로 표현한 자료가 되겠습니다.
오늘 통계학을 공부하기에 앞서 통계학의 본질이 무엇이며 어떠한 철학적 배경이 뒷받침되어야 하는지를 살펴보고 있습니다.
그렇다면 위의 3가지 자료들을 모두 '통계학'이 쓰인 예시라고 말할 수 있을까요?
우리는 통계자료와 통계학을 구분해야 합니다. 가장 중요한 구분 지점은 바로 "정리 및 예측 유무"입니다. 통계자료는 예측을 한 숫자를 모아둔 것이 아니라, 과거나 현재에 발생한 어떤 일에서 나타난 숫자들을 여러 항목에 따라 수집한 것입니다. 반면, 통계학은 이 자료를 바탕으로 한 발 더 나아가고자 하는 방법론이기에 통계자료 속 여러 숫자들로 의미 있는 숫자(결과)를 만들어내고자 합니다. 그러니 통계학이 쓰인 예시라 하면 단순히 수집된 자료가 아닌, 어떤 기법에 따라 의미 있게 축약된 결과가 되어야 할 것입니다.
그럼 다시 각 자료(=데이터(Data))를 살펴보겠습니다.
1. 경기도 수원시의 날씨
이 자료는 통계학이 적용된 결과라고 얘기할 수 있습니다. 과거 및 현재에 수집된 기온 자료들을 바탕으로 통계적 추론(inference)을 하여 아직 경험하지 못한 날씨를 예측하고 있으니까요. 그렇다면, 자료를 바탕으로 예측했다는 이유로 이 자료에 통계학이 쓰였다고 판단하고 있으니 통계학의 특성 중 하나는 "예측"이라고 말할 수 있겠습니다.
2. 미국 중간선거(2022.11.08.)
이 자료에는 통계학이 아주 적게 적용되었습니다. 이미 벌어진 선거의 결과를 수집해서 보기 좋게 풀어낸 것이기 때문입니다. 선거와 관련하여 통계학이 적용된 자료라면, 선거 전 어느 지역에서 어느 당 소속의 후보가 당선될 것이라고 예측하는 미래지향적인 자료 등이어야 할 것 같네요. 다만 미국 인구가 매우 많으니 각 주의 후보별 득표수가 상당히 많을 텐데, 일반적으로 사람들은 득표수보다는 당선 여부에 관심이 있으니 미국 지도 위에 당선인들의 정당을 직관적으로 표현한 것은 좋은 시각화라고 평가할 수 있겠습니다.
3. 삼성전자 주가
이 자료에도 통계학이 아주 적게 적용되었습니다. 지나간 나날들의 주가를 기록해둔 것에 불과하니까요. 기술통계량에 해당하는 '평균 거래량' 정도는 통계학을 적용한 결과라고 볼 수는 있겠습니다. 만약 통계학을 활용하여 주가를 "분석"한 자료가 되려면, 시계열분석(TSA, Time Series Analysis)과 같은 기법을 적용하여 위의 자료에 드러난 표면적인 지표(총 시가, 주가수익비율 등)보다 더 유의미한 결과를 알려주는 모종의 숫자를 도출해 내야 할 것 같습니다.
예측과 분석은 어떠한 현상을 설명하기 위해 필요합니다. 설명은 주장 또는 설득을 위해 필요할텐데, 나의 주장에 상대방이 동의하도록 만들려면 상대방이 쉽게 이해하면서도 반박의 여지없이 논리적인 근거가 필요하지 않을까요?
이때 통계학은 설명에 있어 좋은 논거를 제공합니다. 세상이 모두 숫자로 설명될 수는 없겠지만, 숫자만큼 직관적이고 확실한 근거는 없기 때문이죠. 결국 통계학의 목표는 "의사결정"일 것입니다. 살아가면서 직면하는 많은 선택의 순간에서, 적은 비용을 들여 확실한 근거를 갖고 후회없는 선택을 하기 위해 통계학이 발전한 것이 아닌가 하는 생각이 듭니다.
What is Statistics?
학문적으로 통계학은 스스로를 어떻게 정의하는지 살펴보겠습니다.
the science of collecting, analyzing, presenting, and interpreting data
- Britanica
자료 수집, 정리, 요약 뿐만 아니라 수집한 자료(표본, Sample)에서 얻은 자료로부터
자료를 뽑았던 대상 전체(모집단, Population)에 대한 정보로 바꾸는 작업
- 강상욱 외 9인(2014), EXCEL, SPSS, R로 배우는 통계학 입문, 자유아카데미
The mathematics of the collection, organization, and interpretation of numerical data,
especially the analysis of population characteristics by inference from sampling
- American Heritage Dictionary
정의하는 방식이 매우 다양하지만 같은 이야기를 하고 있습니다. 자료를 모아서 분석하고 해석하는 일련의 과정이기도 하고, 표본으로 모집단의 특성을 추론하는 과정이기도 하고, 뭔가 수학을 빼놓으면 안 될 것 같기도 합니다. 장황하기도 하고 뭔가 어렵기도 하네요.
위의 3가지 예시들을 다시 살펴보면서 통계학의 틀에 대한 감을 잡아봅시다. 2,3번 자료의 경우 뭔가 추측을 하는 과정을 가정해 볼까요?
| 관심 분야 | 수집한 자료 | 관심 목표 | 표현방법 | |
| 1. 경기도 수원시의 날씨 |
경기도 수원시의 기상 |
수원시의 어느 기상관측소에서 측정한 기온, 강수량 등 | ex. 내일 비가 오는가? | 기온 변화 추이, 그림(해, 달, 구름, 비, 눈 등) 등 |
| 2. 미국 중간선거 결과 | 미국의 상원의원 구성 | 과거 상원의원의 득표수, 득표율, 소속 정당 및 선거운동방식, 공약 등 | ex. 내가 지지하는 후보가 당선될 것인가? | 히스토그램, 지도 시각화 등 |
| 3. 삼성전자 주가 | 삼성전자의 주가 흐름 | 과거 주가 등락, 시기별 사건, CEO의 발언 및 행보 등 | ex. 주가는 오를 것인가? | 주가 변화 추이, 기술통계량과 같은 숫자 지표 등 |
통계학은 위 도표의 '관심 목표'와 같은 질문에서 시작합니다. 그래야 원하는 정보를 얻기 위한 자료(표본, Sample)를 수집하고 세부 기법을 설정하여 '관심 분야'(모집단, Population)에 대한 정보를 적절하게 추측(추정(Estimation) 또는 추론(Inference))할 수 있기 때문입니다. 그렇게 알아낸 정보를 보기 좋게 표현하여 상대방과 쉽게 의사소통하기 위해 적절한 '표현 방법'(시각화, Visualization)도 정해야 하겠습니다.
관심 분야에 관한 정보를 모두 수집해서(전수조사) 알아내고자 하는 것을 알아내면 좋겠지만, 현실적으로 시간과 돈이 많이 들 것입니다. 따라서 관심 분야에 관한 자료 중 일부분(표본집단)만을 수집해서 "효율적으로" 전체에 관한 정보(모수, parameter)를 추론하는 것이 좋겠죠? 이것이 바로 통계학의 기본 구조가 되겠습니다. 이때 효율적으로 자료를 분석하고 추론을 해내는 방법에는 여러 가지가 있습니다. (앞으로 이것에 대해 차근차근 다뤄봅니다.)
최근에는 소프트웨어를 통해 그림, 도표 등 더욱 쉽게 상황을 파악할 수 있는 시각화 기법도 많이 존재합니다. 그리고 모델을 구축하고 예측, 분류, 판단을 해내기 위해 통계분석과 소프트웨어공학을 종합적으로 활용하는 데이터사이언스(Data Science)도 매우 빠르게 발전하고 있습니다.
요약 및 용어정리
- 통계학은 표본집단으로 모집단의 특성(모수, parameter)을 추론하는 과정이며, 그 과정에서 발생하는 오차를 줄이는 방법을 연구하는 학문이다.
- 통계학은 어떤 현상을 설명하기 위해 활용하는 도구이다.
- 통계학은 자료에서 한 발 더 나아가 예측적인 숫자를 도출하려는 방법론이다.
- 모집단(Population) : 관심 분야에 대한 자료(데이터) 전체.
- 모수 : 모집단의 특성을 표현하는 지표. 최종적으로 추정하고자 하는 것(모평균, 모분산, 모표준편차 등).
- 표본집단 : 모집단의 자료 중 일부분만 수집한 자료.