본 게시글에서는 논문 Sagawa et. al.(2020) <Distributionally Robust Neural Networks for Group Shifts: On the Importance of Regularization for Worst-Case Generalization> 을 리뷰합니다.
Background
1. 허구적 상관관계
Spurious correlation(허구적 상관관계)란, 관심이 있는 어떤 변수 X와 변수 Y가 존재할 때, X와 Y에 모두 영향을 주는 또 다른 변수(이른바 '혼재변수(Confounding Variable)')로 인해 X와 Y 간에 인과관계가 있는 것처럼 보이는 상황을 의미합니다. 전통적인 통계학과 최근의 머신러닝에서는 Confounding Variable을 없애고 변수 X와 Y 간의 진정한 인과관계를 찾기 위한 다양한 방법을 논의해왔습니다.
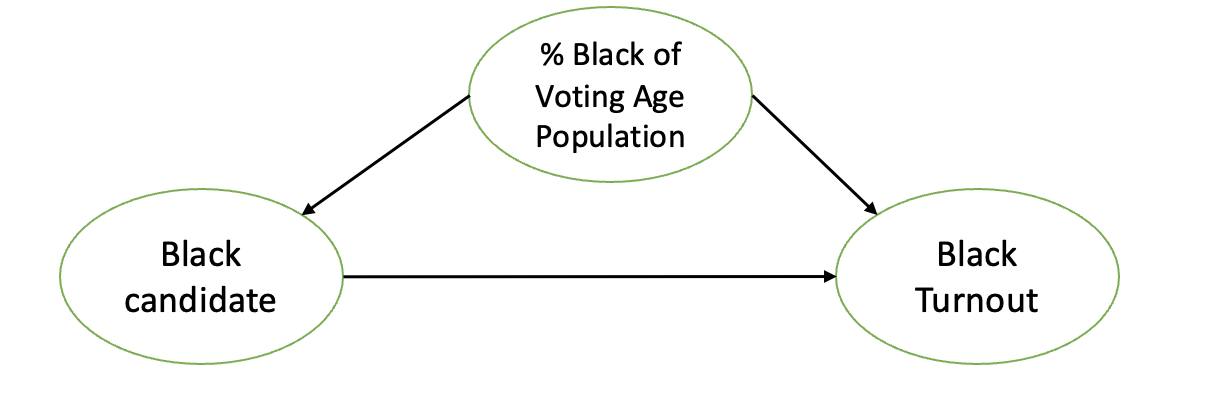
예를 들어볼까요? 미국의 흑인 피선거권자 수(변수 \(X\))가 많아질수록, 흑인 인구의 투표율(변수 \(Y\))이 어떻게 변화하는지 예측하는 단순선형회귀분석의 상황을 가정해봅시다. 수식은 이렇게 쓸 수 있겠습니다.
$$ Y_i = \beta_0 + \beta_1 X_i + \epsilon_i \qquad (\epsilon_i \sim N(0,\sigma^2)) $$
그런데 이때, 미국의 흑인 선거가능인구 비율(변수 \(Z\))는 미국의 흑인 피선거권자 수(변수 \(X\))와 미국의 흑인 투표율(변수 \(Y\))에 모두 영향을 줄 것입니다. 따라서 회귀분석에서는 \(X\)와 \(Y\)간의 진정한 인과관계만을 알아내기 위해서, \(X\)가 \(Z\)를 거쳐 \(Y\)로 가는 인과관계('route')를 배제해야만 하겠습니다. 가장 쉬운 해결방법은 변수 \(Z\)를 위의 회귀모형에 추가하여, 변수 \(X\)의 회귀계수인 \(\beta_1\)만을 관찰해내는 것입니다.
$$ Y_i = \beta_0 + \beta_1 X_i + \beta_2 Z_i +\epsilon_i \qquad (\epsilon_i \sim N(0,\sigma^2)) $$
2. 알고리즘의 불공정성(unfairness)

머신러닝/딥러닝 알고리즘이 실생활에서 유용하게 쓰이는 분야가 바로 '안면인식(Facial recognition)'입니다. 미국에서는 이 알고리즘이 실제로 CCTV 또는 몽타주를 바탕으로 피의자를 규명하는 데에 사용되고 있는데요, 이 알고리즘이 무고한 시민의 얼굴을 피의자의 얼굴이라고 잘못 판단하는 사건이 발생합니다. 미국 경찰의 안일한 업무 처리도 문제였지만, 편향된 데이터로 학습한 알고리즘이 주된 원인이었으며 무고한 시민과 그의 가족은 알고리즘의 오류가 판명될 때까지 굴욕적인(humiliating) 시간을 보내야 했습니다. (자세한 사건이 궁금하시면 뉴욕타임스의 기사를 읽어보세요)
실제로 'African-American male'에 대한 데이터는 'European-American male'에 대한 데이터가 역사적으로 적을 수밖에 없으며, 'female'에 대한 데이터 역시 'male'에 대한 데이터보다 역사적으로 적을 수밖에 없습니다. 따라서 데이터에서 추출(extract)해낼 수 있는 특징들(feature)의 세분화 정도가 인종/성별 등의 그룹(group)에 따라 달라질 수밖에 없고, 이것은 이전엔 예측하지 못했던 허구적 상관관계들이 가득한 '불공정한 알고리즘(unfair algorithm)'을 만들어냅니다.
따라서 최신 머신러닝 연구에서는 공정한 알고리즘을 만들기 위해 다양하게 시도하고 있으며, 이번 게시글에서 다루는 논문도 그러한 시도 중 유의미한 하나의 연구가 되겠습니다.
Distribution Robust Optimization(DRO)
머신러닝/딥러닝의 목표는 모델의 손실함수(loss function) 값(loss)을 최소화하면서, 분류(classification) 또는 회귀(regression) 등의 과제를 수행하는 성능(accuracy)을 최대화하는 것입니다. 그런데 전통적으로 인공신경망(Neural Network)은 'iid 가정(independent and identically distributed)'에 의한 데이터셋에서 성능이 높았기에, 적은 수의 표본들에 대해서나, 조금씩 다른 분포의 표본들에 대해서도 좋은 성능을 내는 모델을 만들기 위해 어떻게 해야할 것인지에 대한 연구들이 최근 부상하기 시작했습니다. 즉, 어떠한 분포의 표본들(이른바 'Distribution shift'의 상황)이 입력되더라도 항상 견고한(Robust) 성능을 유지하는 최적화(Optimization) 방법이 머신러닝에서 또 하나의 연구 분야로 자리매김한 것이죠.
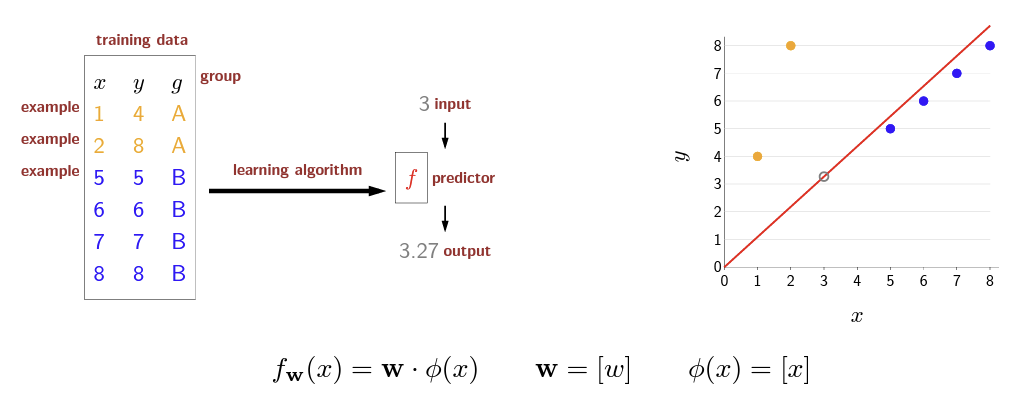
직관적인 문제 인식을 위해, 위와 같은 간단한 선형회귀 상황을 생각해보겠습니다. 평소에 그래왔듯이 딥러닝에서는 오차역전파법(Backpropagation)과 경사하강법(Gradient Descent)을 사용하여 모델 \(f\)의 기울기 \(\boldsymbol{w}\)를 추정할 것입니다. \(\phi(x)\)는 kernel을 뜻하는데, 여기서는 선형 근사를 하는 상황이므로 \(y=x\)라고 간단히 설정한 것입니다.
목표는 손실함수를 최소화하는 것이므로, 모델의 손실함수를 MSE(Mean square estimator) = \((\hat{\theta}-\theta)^2\)로 설정하고 기울기 \(\boldsymbol{w}\)가 1이라고 생각했을 때 average training loss를 계산해보겠습니다.
$$ TrainLoss(\boldsymbol{w}=1) = \frac{1}{6}((1-4)^2+(2-8)^2+(5-5)^2+(6-6)^2+(7-7)^2+(8-8)^2)=7.5 $$
그런데, 위의 모델 학습에서는 데이터 \((x,y)\)가 그룹 A와 B로 나뉘어있다는 정보를 활용하지 않았습니다. 그러다면 이른바 'per-group training loss'를 구해보면 어떨까요?
$$ TrainLoss_A(\boldsymbol{w}=1) = \frac{1}{2}((1-4)^2+(2-8)^2)=22.5 $$
$$ TrainLoss_B(\boldsymbol{w}=1) = \frac{1}{4}((5-5)^2+(6-6)^2+(7-7)^2+(8-8)^2)=0 $$
즉, 위의 일반적인 모델 학습에서는 그룹 A에 대한 정보가 모두 손실되고 있었다는 것을 알 수 있습니다. 앞서 소개한 'Wrongfully Accused by an Algorithm' 기사의 사건도 바로 이런 상황을 고려하지 않고 학습된 알고리즘을 안면인식에 활용하는 바람에 발생한 문제라고 직관적으로 이해할 수 있겠죠.
이것을 해결하기 위해 고안된 'Group DRO' task는 손실함수로 'maximum group loss'를 사용할 것을 제안합니다. 즉, 그룹별로 손실을 계산한 후, 그 중 최댓값을 모델 전체의 손실로 인식하여 이것을 최소화하는데 주력하자는 것입니다. 그림과 수식으로 표현하면 이렇습니다.

$$ \nabla TrainLoss_{max}(\boldsymbol{w}) = \nabla TrainLoss_{g^{*}}(\boldsymbol{w}) \qquad (g^{*}=arg \underset{g}{max} TrainLoss_g(\boldsymbol{w}))$$
"Strongly-regularized" group DRO
Sagawa et al.(2020)은 논문에서 DRO를 만약 'overparameterized model(초과매개변수화된 모델)', 즉 모종의 이유로 과적합(overfitting)된 모델에 적용하게 되면 일반적인 모델 손실(average training loss)과 'worse-case training loss'가 같아지므로 group DRO가 무의미할 수 있다고 주장하며 문제를 제기합니다(이것을 논문에서는 'vanishing-training-loss regime'이라고 일컫습니다). 따라서 위의 group DRO 또한 인공신경망의 일반화 문제(generalization in neural networks)를 완전히 해결할 수 없으며, 논문에서 제안하는 'Strongly-regularized group DRO'가 이러한 상황을 해결하는 새로운 시각을 제시한다고 주장합니다.
1. 이론 및 수식 정리
가능한 모델들의 family를 \(\Theta\)라고 하고, 그 안의 원소(모델)를 \(\theta\)라고 지칭하겠습니다. \(x\)로 \(y\)를 예측(회귀)하거나 \(x\)를 \(y\)로 분류하는 과제를 수행하기 위해 필요한 데이터 \((x,y)\)가 어떤 분포 \(P\)를 따른다고 할 때, 훈련 데이터의 empirical distribution을 \(\hat{P}\)라고 하겠습니다. 그러면 일반적으로 우리가 구하고자 하는 모델을 수식으로 표현하면 다음과 같습니다.
$$ \hat{\theta}_{ERM} := arg \underset{\theta \in \Theta}{min} \mathbb{E}_{(x,y) \sim \hat{P}} [l(\theta ; (x,y))] $$
여기서 ERM이란 'Empirical Risk Minimization'으로, 한정되어 있는 훈련 데이터를 가지고 모델의 Risk를 최소화하는 과정을 지칭하는 용어입니다.
그렇다면 위에서 소개한 group DRO로 구한 모델을 수식으로 표현하면 어떨까요? 바로 이렇습니다.
$$ \hat{\theta}_{DRO} := arg \underset{\theta \in \Theta}{min} \{ \underset{g \in \mathcal{G}}{max} \mathbb{E}_{(x,y) \sim \hat{P}} [l(\theta ; (x,y))] \} $$
여기서 \(\mathcal{G}\)는 발생할 수 있는 모든 group을 모아둔 집합(논문에서는 모든 group의 인덱스 숫자를 모아둔 집합)이라고 생각하면 되겠습니다. 논문에서는 실험과 설명을 위한 데이터셋으로 'Waterbirds dataset', 'CelebA dataset', 'MultiNLI dataset'을 사용하고 있는데요, 예를 들어 Waterbirds dataset에서 주어지는 이미지 \(x\)를 waterbird와 landbird를 구분하고자 한다면 \(\mathcal{Y}\)={waterbird, landbird}가 됩니다. 그리고 이때 'confounding variable'이라고 볼 수 있는 'spurious attribute'는 \(\mathcal{A}\)={water background, land background}가 될텐데요, 따라서 이 데이터셋을 이용한 과제에서 따져야 할 group의 수는 \(n(\mathcal{G}) = 2 \times 2 = 4\)개가 됩니다.
이때, 논문은 손실함수 \(l(\theta;(x,y))\)에 (1) L2-norm penalty \(\lambda || \theta ||_{2}^{2} \)를 적용하고(이른바 'Structural risk minimization(Vapnik and Chervonekis, 1974)', (2) 모델 학습 시 epoch을 작게('early stopping', 논문의 실험에서는 epoch=3 정도) 했을 때, 모델의 성능을 높이면서도 그룹 간의 일반화 정도가 함께 높아진다고 주장합니다. 이른바 'Generalization gap' \(\delta = R(\theta) - \hat{R}(\theta)\)을 줄일 수 있다는 것이죠.
그리고 (3) 그룹 간의 편차를 줄이기 위한 시도('group adjustment')도 추가합니다. 수식으로 표현하면 이렇습니다.
$$ \hat{\theta_{adj}} := arg \underset{\theta \in \Theta}{min} \{ \underset{g \in \mathcal{G}}{max} \mathbb{E}_{(x,y) \sim \hat{P}} [l(\theta ; (x,y))] + \frac{C}{\sqrt{n_g}} \} $$
이때 상수 \(C\)는 'model capacity constant'라고 부르는 상수이자 hyperparameter이고, '\(n_g\)는 그룹별 표본의 크기입니다. 즉, 표본의 크기가 작을수록 과적합(overfitting)의 가능성이 커지기 때문에, 이것을 보정하기 위해 추가로 넣은 숫자로 생각하면 되겠습니다. 참고로 ERM에서는 group을 따지지 않기 때문에, 수식에 추가되는 분수꼴은 통으로 상수 처리가 되어서 최적화에 영향을 주지 않습니다.
2. 실험(Experiments)

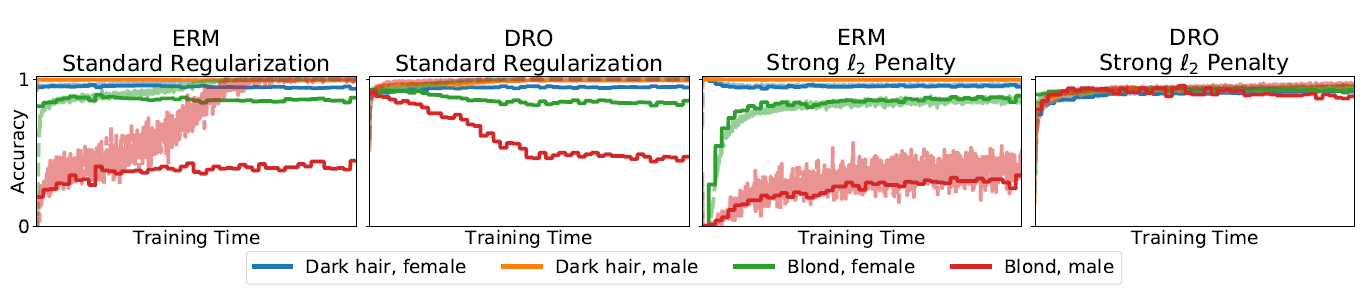
앞서 언급한 바와 같이 3개의 데이터셋으로 각각의 실험을 수행하였습니다. Waterbirds dataset과 CelebA dataset을 이용한 ResNet50 모델로 이미지를 인식하는 과제를, MultiNLI dataset을 이용한 BERT 모델로 두 문장의 어조를 비교하여 분류(entailment/netural/contradiction)하는 과제를 수행하였는데, CelebA dataset을 이용한 모델 성능 그래프(Figure 2)로 알 수 있듯이 L2-penalty를 부여한 DRO에서 그룹 4개에 관계없이 일정하게 높은 training / validation 성능을 보이고 있었습니다.
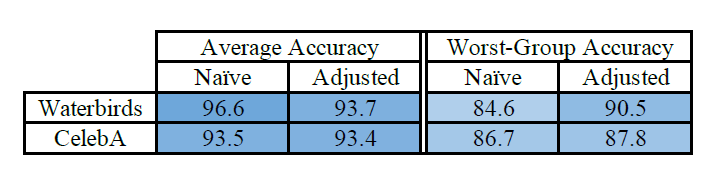

그리고 group adjustment를 적용했을 때, 물론 모델의 성능이 다소 낮아지긴 하였으나, 모델 간의 'Generalization gap'이 더욱 줄어들었음을 확인할 수 있었습니다(Table 2). 그리고 L2-penalty에 필요한 \(\lambda\)와 model capacity constant인 \(C\)는 hyperparameter이므로 우리가 직접 설정해야 하는데, Waterbird dataset을 이용한 과제에서는 \(\lambda=1.0\)이고 \(C=2\)일 때 가장 우수한 일반화 정도를 나타내는 것을 실험으로 확인하였습니다.
3. 학계에의 기여(Contributions)
본 논문은 보통 훈련 데이터의 분포와 테스트 데이터의 분포가 다를 때 사용하는 'Importance weighting(Upweighting)'의 방법보다도 성능이 좋음을 이론적으로, 그리고 경험적으로 증명했습니다. importance-weighted estimator는 손실함숫값에 그룹별로 가중치 \(w_g\)를 곱한 값을 평균내었을 때 그것을 최소화하는 모델이 됩니다. 즉, 수식으로 표현하면 이렇습니다.
$$ \hat{\theta_{w}} := arg \underset{\theta \in \Theta}{min} \{ \mathbb{E}_{(x,y,g) \sim \hat{P}} [w_g l(\theta ; (x,y))] \} $$
이때 이 그룹별 가중치는 그 그룹이 empirical distribution인 \(\hat{P}\)를 따를 확률의 역수로 설정하는데, 이렇게 되면 표본의 크기가 작은 그룹들(minority groups)에 더 가중치가 매겨지게 되는 것이죠.
그런데 이렇게 지정하면 실제로 실험을 해보았을 때 Group DRO에 비해 일정하게 낮은 손실이 발생하지는 않는다는 것을 관측할 수 있었습니다(Table 3).

더불어, 이론적으로는 importance weighting과 DRO에서의 모델이 convex하면 어떤 가중치(importance weight)에서는 결과적인 모델(estimator \(\hat{\theta}\))이 같아질 수 있는데, 만약 이 모델이 non-convex하면 그렇지 않음을 증명했습니다. 즉, 모델 \(\theta\)가 non-convex하면, 견고한(robust) estimator \(\hat{\theta}_w\)를 만들어내는 가중치 해를 구할 수 없다는 것이죠. 반면에 DRO는 모델의 convex 여부에 관계없이 사용할 수 있으므로, 더욱 범용적인 방법이 됩니다.
따라서, 본 논문에서 제안한 방법(strongly-regularized group DRO)으로 전반적인 모델의 성능(average accuracy)은 조금 낮아질지라도 손실이 최대화되는 group에 적용되는 모델의 성능(worst-case accuracy)을 상당히 높일 수 있는 방법입니다. 궁극적으로 이 방법은 Distribution shift가 발생하더라도 모델의 Over-confidence를 소거하고 결과의 일반화(Generalization)를 함양할 수 있는 새로운 시각을 제공한다고 볼 수 있겠습니다.
Reference
연세대학교 정치외교학과 김정현 교수님 강의(정치학데이터분석)
Stanford CS221 - Group DRO
Distributionally Robust Neural Networks for Group Shifts: On the Importance of Regularization for Worst-Case Generalization
Overparameterized neural networks can be highly accurate on average on an i.i.d. test set yet consistently fail on atypical groups of the data (e.g., by learning spurious correlations that hold on average but not in such groups). Distributionally robust op
arxiv.org
Empirical Risk Minimization(경험적 위험도 최소화)
End-to-End Deep Learning task - 해결할 일(task)에 대해 분석한다 - 이와 관련된 데이터를 이해한다(...
blog.naver.com
댓글