확률분포는 왜 필요한가?
우리는 보통 어떤 사건의 발생 가능성을 알고 싶을 때 '확률'의 개념을 많이 활용합니다. Frequentist의 입장에서, 확률이라는 숫자에 객관성을 보장하려면 확률실험(Random experiment)을 거쳐야만 하죠. 아래의 3가지 조건을 만족해야 random experiment라고 할 수 있겠습니다.
(1) 시행으로 가능한 결과들을 모두 알아야 한다(=표본공간을 정의할 수 있어야 한다).
(2) 한 시행의 결과를 딱 한 개로 정확하게 예측할 수 없어야 한다.
(3) 동일한 조건에서 동일한 결과가 나오는 시행을 무한 반복할 수 있어야 한다.
사실 (1)과 (2)는 어떻게든 가능하다고 할지라도, 인간의 삶은 유한하기 때문에 (3)이 많은 경우에 불가능합니다. 따라서 많은 경우에 (3)이 가능하다고 가정하고, 실험 결과로 얻어진 숫자(확률)를 각종 의사결정에 중요한 참고자료로 활용합니다.
이때 수많은 random experiment의 상황들을 범주화하여 간단명료하게 표현한 것이 바로 확률분포입니다. 따라서 우리가 궁금한 상황이 미리 규정된 어떤 분포에 해당함을 알게 되면, 확률 계산과 의사소통이 매우 편리해집니다. 물론 현실적으로 어려운 일입니다.
확률분포 조감도
전통적인 확률분포들을 간단하게 분류해보면 아래와 같습니다. 직접 그리느라 조금 고달팠네요..


구체적으로 하나씩 살펴보겠습니다. 이 글에서는 먼저 확률변수가 어떤 사건의 발생(성공)횟수일 때의 분포를 정리합니다.
이산확률분포
1. 확률변수 \(X\)가 어떤 사건의 발생(성공) 횟수일 때
1) 베르누이분포(Bernoulli Distribution)
스위스의 수학자 야코프 베르누이(Jacob Bernoulli)는 고전주의 학파(라플라스류)의 확률론이 정립되는 데에 아주 크게 기여한 사람입니다. 그의 저서 Ars Conjectandi(1713)에서 '베르누이 시행(Bernoulli trial)'이라는 개념이 처음으로 등장하는데, 이는 시행 결과가 무작위적(random)으로 성공(success) 또는 실패(fail) 두 가지만 있는 사건(표본공간 = {성공, 실패})을 수행하는 행위를 뜻합니다(이러한 행위에 대해서 나중에 베르누이의 이름을 본따 베르누이 시행이라고 명명되었습니다). 이전에 통계학의 본질탐구(2)에서 확률론의 시초는 도박이라는 이야기를 했었는데, 내가 돈을 딸 것인가 잃을 것인가에 대한 관심이 베르누이 시행을 정의하는 것으로 이어졌다고 판단해도 무방하겠습니다.
베르누이 시행과 관련된 확률분포에서는 (쉬운 이해를 위해) 두 가지의 결과를 성공과 실패로 지칭하는데, 사실 어떤 사건이 발생했느냐 안 했느냐로 파악하는 것이 더 직관적이고 정확할 것 같습니다. 그래야 추후 경우의 수가 더 많아지는 확률분포를 조금 더 잘 받아들일 수 있기 때문이죠.
\(X \sim Bernoulli(p)\)
이산확률변수 \(X\) : 성공횟수(사건의 발생횟수) = 0 또는 1
모수(parameter) \(p\) : 성공확률(사건의 발생확률)
확률질량함수(pmf) \(f_X(x)=p^{x}(1-p)^{1-x}\)
평균 \(E(X)=p\)
분산 \(Var(X)=p(1-p)\)
베르누이분포는 베르누이 시행을 한 번만 했을 때 발생하는 확률을 나타내기 때문에, 확률변수가 될 수 있는 숫자는 0 또는 1밖에 없겠습니다. 따라서 확률질량함수의 함숫값도 \(p\) 또는 \(1-p\)밖에 없습니다. 이때 베르누이 시행을 여러 번(n회) 하게 되면, 비로소 이항분포 또는 초기하분포가 되는 것입니다.
2) 이항분포(Binomial Distribution) : n회 복원추출(with replacement, 각 베르누이 시행이 독립사건)
베르누이 시행을 여러 번(n번) 반복하는 경우를 이항분포라고 정의합니다. 그러니 이제 어떤 사건을 총 몇 번(\(n\)) 수행하는지도 알아야 하기 때문에 \(n\)도 확률질량함수의 함숫값(결과확률)에 영향을 주는 모수로 판단합니다. 이때 중요한 것은 성공확률(사건의 발생확률) \(p\)인 베르누이 시행을 n회 반복할 때 각 시행이 독립적으로 이루어진다는 것이죠. 이는 시행이 반복되어도 표본공간에 변화가 없다는 뜻입니다. 따라서 조합(combination) 개념을 이용하여 경우의 수와 확률을 따져야 하는데, 이때 확률을 계산하는 식이 이항정리와 같아서 이항분포라는 이름이 붙었습니다.
동전 던지기를 3번(\(n=3\) 반복하는 상황을 가정해볼까요? 동전의 앞면이 나오는 횟수를 확률변수 \(X\)로 정의하면, 가능한 경우의 수로 이산확률분포표를 그려보았을 때 아래와 같습니다.
| 확률변수 X (앞면이 나오는 횟수) |
경우의 수 | 확률 계산 |
| 0 | (뒤, 뒤, 뒤) | \(_3C_0 (\frac{1}{2})^0(1-\frac{1}{2})^{(3-0)}=\frac{1}{8}\) |
| 1 | (앞, 뒤, 뒤) (뒤, 앞, 뒤) (뒤, 뒤, 앞) |
\(_3C_1 (\frac{1}{2})^1(1-\frac{1}{2})^{(3-1)}=\frac{3}{8}\) |
| 2 | (앞, 앞, 뒤) (앞, 뒤, 앞) (뒤, 앞, 앞) |
\(_3C_2 (\frac{1}{2})^2(1-\frac{1}{2})^{(3-2)}=\frac{3}{8}\) |
| 3 | (앞, 앞, 앞) | \(_3C_3 (\frac{1}{2})^3(1-\frac{1}{2})^{(3-3)}=\frac{1}{8}\) |
\(X \sim Bin(n,p)\)
이산확률변수 \(X\) : 성공횟수(사건의 발생횟수)
모수(parameter) \(n\) : 전체 시행횟수
모수(parameter) \(p\) : 성공확률(사건의 발생확률)
확률질량함수(pmf) \(f_X(x)=\displaystyle \binom{n}{x}p^{x}(1-p)^{n-x}\)
평균 \(E(X)=np\)
분산 \(Var(X)=np(1-p)\)
조합 표기를 보통 \(_nC_x\)같이 하지만, 확률론에서는 \(\binom{n}{x}\)로도 많이 합니다. 또, \(Binomial(n,p)\), \(Bin(n,p)\), \(B(n,p)\) 모두 같은 표기입니다.
상황 예시)
◇ 사건 = 동전 던지기 → \(p=\frac{1}{2}\), 시행결과(표본공간) = {앞면, 뒷면}
◇ 사건 = 주사위를 던져서 3이 나오기 → \(p=\frac{1}{6}\), 시행결과(표본공간) = {3, 3이 아닌 것}
3) 초기하분포(Hypergeometric Distribution) : n회 비복원추출(without replacement, 각 베르누이 시행이 독립시행이 아님)
베르누이 시행이 n회 반복되는 것은 맞는데, 시행을 거치면서 표본공간이 계속 바뀌는 경우(=비복원추출)의 확률분포를 초기하분포라고 합니다. 직관적인 이해를 위해, 10개의 구슬이 들어있는 주머니(=모집단)의 상황을 가정해볼까요?
Q. 주머니 안에 10개의 구슬이 있고, 그 중 4개의 구슬이 옥구슬이고 나머지는 플라스틱 구슬이다. 주머니에서 구슬을 뽑을 기회가 4번 주어졌을 때, 옥구슬을 2개 뽑을 확률을 구하시오.
구슬을 뽑는 행위는 비복원추출(without replacement)에 해당합니다. 뽑은 구슬을 주머니에 다시 넣지 않기 때문이죠. 그렇다면 조합(combination) 개념을 이용해서 아래처럼 확률을 계산할 수 있습니다.
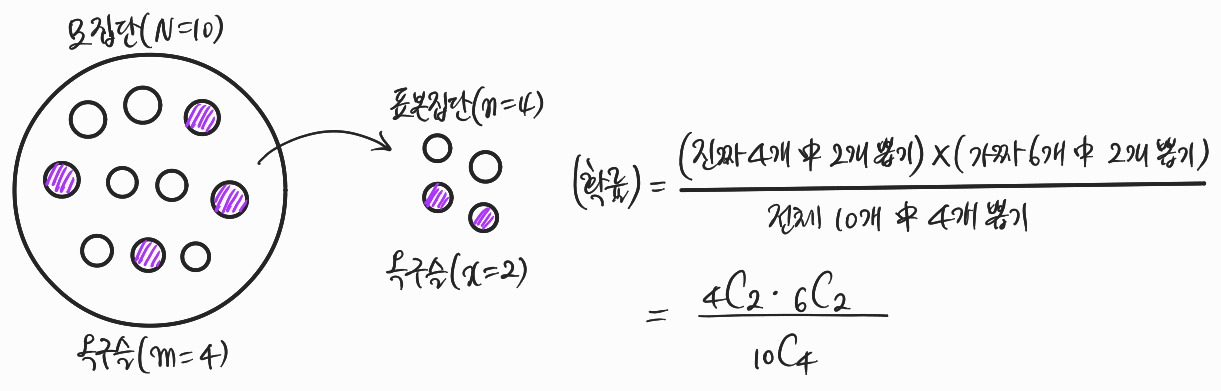
여기서 '뽑고자 하는 진짜 옥구슬의 개수'만 변수 \(x\)로 두면 초기하분포의 확률질량함수가 된답니다.
\(X \sim Hypergeo(N,m,n)\)
이산확률변수 \(X\) : 표본집단 원소 중 원하는 사건의 발생 횟수(성공횟수)
모수(parameter)\(N\) : 모집단의 총 원소 개수(가능한 모든 사건의 개수)
모수(parameter) \(m\) : 모집단 원소 중 원하는 사건의 개수(성공횟수)
모수(parameter) \(n\) : 표본집단의 총 원소 개수(가능한 모든 사건의 개수)
확률질량함수(pmf) \(f_X(x)=\displaystyle \frac{\displaystyle \binom{m}{x}\dot \displaystyle \binom{N-m}{n-x}}{\displaystyle \binom{N}{n}}\)
평균 \(E(X)=n \displaystyle \frac{m}{N}\)
분산 \(Var(X)=n \displaystyle \frac{m}{N} \frac{N-m}{N} \frac{N-n}{N-1}\)
4) 다항분포(Multinomial Distribution) : 이항분포의 일반화
앞서 살펴본 베르누이분포, 이항분포, 초기하분포 이 세 가지는 '성공'과 '실패' 두 가지만 표본공간에 존재하는 베르누이 시행을 바탕으로 설계된 확률분포였습니다. 이때 발생 가능한 모든 \(k\)개 베르누이 시행의 개별 성공확률을 모두 따지는 확률분포를 다항분포라고 합니다. 그래서 앞의 세 분포와 달리 확률변수 \(X\)는 \((X_1,X_2,\cdots,X_k)\)와 같은 벡터 형태이고(단, 값이 0 또는 1), \(k\)개 사건의 개별 성공 확률이 모두 다르므로 모수도 \(p_1,p_2,\cdots,p_k\)와 \(n\)으로 상당히 많습니다.
\(X=(X_1,\cdots,X_k) \sim Multinomial(n,p_1,p_2,\cdots,p_k)\)
이산확률변수 \(X=(X_1,\cdots,X_k)\) : 총 \(k\)개의 사건 각각의 성공횟수(발생횟수) = 0 또는 1
모수(parameter) \(n\) : 전체 시행횟수
모수(parameter) \(p_1,\cdots,p_k\) : \(k\)개의 사건 각각의 성공확률(발생확률)
확률질량함수(pmf) \(f_X(x)=\displaystyle \frac{n!}{x_1!x_2! \cdots x_k!} {p_1}^{x_1} {p_2}^{x_2} \cdots {p_k}^{x_k}\)
\( where \sum_{i=1}^{k}X_i=n, \sum_{i=1}^{k}p_i=1\)
\(i\)번째 사건에 대하여 평균 \(E(X_i)=np_i\)
\(i\)번째 사건에 대하여 분산 \(Var(X_i)=np_i(1-p_i)\)
5) 포아송분포(Poisson Distribution)
포아송분포는 고정된 단위시간(또는 공간) \(\lambda\)동안 어떤 사건이 몇 번 성공(발생)할 확률이 궁금할 때 활용하는 분포입니다. 단위시간이나 단위공간은 그냥 어떤 정해진 범위 정도로 받아들이면 되겠습니다. 확률밀도함수는 매클로린 급수와 연관되어 있답니다.
\(e^{\lambda}= \displaystyle \sum_{x=0}^{\infty} = 1 + \lambda + \frac{\lambda^2}{2!} + \frac{\lambda^3}{3!} + \cdots\)
양변을 \(e^{\lambda}\)로 나누면
\(1 = \displaystyle \sum_{x=0}^{\infty} \frac{e^{-\lambda}\lambda^x}{x!}\)
\(x\)가 0보다 클 때 총합이 1이므로, 시그마 옆의 식이 pmf가 될 수 있습니다.
\(X \sim Poi(\lambda)\)
이산확률변수 \(X\) : 사건의 발생 횟수(성공횟수)
모수(parameter) \(\lambda\) : 단위시간 또는 단위공간
확률질량함수(pmf) \(f_X(x)=\displaystyle \frac{e^{-\lambda}\cdot \lambda^{x}}{x!}\)
평균 \(E(X)=\lambda\)
분산 \(Var(X)=\lambda\)
상황 예시)
◇ 궁금한 것 = 한 시간동안 어느 사거리에서 교통사고가 X번 발생할 확률 → \(X \sim Poi(1)\) (시간 단위) 또는 \(X \sim Poi(60)\) (분 단위)
◇ 궁금한 것 = 하루동안 한 전화번호로 걸려온 전화 중 잘못 걸려온 전화가 X번일 확률 → \(X \sim Poi(24)\) (시간 단위) 또는 \(X \sim Poi(24\cdot 60)\) (분 단위)
6) 분포수렴
신기하게도 \(n\)이 무한대로 갈 때 이항분포와 포아송분포는 결국 정규분포에 가까워집니다(=극한분포가 정규분포이다)(=정규 근사). 수리적 증명도 비교적 간단하고, 아주 유용하게 써먹을 수 있는 정리입니다.
▼ Proof ▼
A. \(n \to \infty, p \to 0, np \to \lambda\)이면 이항분포가 포아송분포에 근사 \(X \sim B(n,p) \overset{D} {\rightarrow} Poi(np)\)
\( \begin{align} p_X(x) &= \frac{n!}{x!(n-x)!} p^x (1-p)^{n-x} \\ &= \frac{n!}{x!(n-x)!}(\frac{\lambda}{n})^x (1-\frac{\lambda}{n})^{n-x} \\ &= \frac{\lambda^x}{x!} \cdot \frac{n(n-1) \cdots (n-x+1)}{n^x} \cdot (1-\frac{\lambda}{n})^n \cdot (1-\frac{\lambda}{n})^{-x} \\ & \to \frac{\lambda^x}{x!} \cdot 1 \cdot e^{-\lambda} \cdot 1 \\ &= \frac{\lambda^x e^{-\lambda}}{x!} \end{align} \)
(중간의 분수식은 로피탈의 정리에 의해 1로 수렴, 뒤의 분수식은 각각 자연상수의 정의에 의해 & \(\frac{c}{\infty} \to 0\)에 의해 1로 수렴)
B. \(np\geq 5, n(1-p)\geq 5\)이면 이항분포가 정규분포에 근사 \(X \sim B(n,p) \overset{D} {\rightarrow} N(np,np(1-p))\)
\(X_1, \cdots , X_{\lambda} \overset{iid}{\sim} Bernoulli(p)=Bin(1,p)\) 일 때, \(Y\)를 \(\displaystyle \sum_{i=1}^{\lambda}X_i\)로 두면,
\(Y \sim Bin(n,p)\)
이때 \(\displaystyle \frac{Y}{n} = \displaystyle \frac{1}{n} \sum_{i=1}^{\lambda}X_i = \overline{X} = \) 표본평균 형태! & \(Bin(1,p)=Bernoulli(p)\)를 따르므로 \(E(\frac{Y}{n})=p, Var(\frac{Y}{n})=p(1-p)\)
따라서 \(n\)이 충분히 클 때, 중심극한정리(Central Limit Theorem, CLT)에 의해
\(\displaystyle \frac{\sqrt{n} (Y/n - p)}{\sqrt{p(1-p)}} = \frac{Y-np}{\sqrt{np(1-p)}} \overset{D}{\rightarrow} N(0,1) \)
\(\therefore Y \overset{app}{\sim} N(np, np(1-p))\)
C. \(np=\lambda \to \infty\) 이면 포아송분포가 정규분포에 근사 \(X \sim B(n,p) \overset{D} {\rightarrow} Poi(\lambda=np) \overset{D} {\rightarrow} N(\lambda, \lambda)\)
\(X_1, \cdots , X_{\lambda} \overset{iid}{\sim} Poi(1)\) 일 때, \(Y\)를 \(\displaystyle \sum_{i=1}^{\lambda}X_i\)로 두면,
\(Y \sim Poi(\lambda)\) (서로 독립인 포아송분포 확률변수끼리 더하거나 뺄 수 있음)
이때 \(\displaystyle \frac{Y}{\lambda} = \displaystyle \frac{1}{\lambda} \sum_{i=1}^{\lambda}X_i = \overline{X} = \) 표본평균 형태! & \(Poi(1)\)를 따르므로 \(E(\frac{Y}{\lambda})=1, Var(\frac{Y}{\lambda})=1\)
따라서 \(\lambda\)가 충분히 클 때, 중심극한정리(Central Limit Theorem, CLT)에 의해
\(\displaystyle \frac{\sqrt{\lambda} (Y/\lambda - 1)}{\sqrt{1}} = \frac{Y-\lambda}{\sqrt{\lambda}} \overset{D}{\rightarrow} N(0,1) \)
\(\therefore Y \overset{app}{\sim} N(\lambda,\lambda)\)
Reference
Hogg et.al. (2020). Introduction to Mathematical Statistics(8th Global ed.). London: Pearson.
연세대학교 응용통계학과 박태영 교수님 강의(수리통계학(1))
연세대학교 응용통계학과 강승호 교수님 강의(이론통계학(1))
28.1 - Normal Approximation to Binomial | STAT 414
Enroll today at Penn State World Campus to earn an accredited degree or certificate in Statistics.
online.stat.psu.edu
[기초통계] 초기하분포 의미 및 개념 정리
초기하분포 의미 및 개념 정리
losskatsu.github.io
'Statistics' 카테고리의 다른 글
| 적률생성함수(Moment Generating Function) (0) | 2023.03.05 |
|---|---|
| 통계학의 본질탐구(4) Frequentist & Bayesian 2 (0) | 2023.02.18 |
| 통계학의 본질탐구(3) Frequentist & Bayesian 1 (0) | 2023.02.14 |
| 통계학의 본질탐구(2) 철학적 기원 (1) | 2023.01.30 |
| 통계학의 본질탐구(1) communication, Myth & Truth, Inspiration, necessity (0) | 2023.01.23 |




댓글