통계학의 본질탐구(4) Frequentist & Bayesian 2

** 통계학의 역사에 관심이 있으시다면, 아래 글을 먼저 읽고 오시면 더 좋아요!

통계학의 본질탐구(2) 철학적 기원

통계학의 본질탐구(3) Frequentist & Bayesian 1

 

 

 

200년간의 논쟁

 

 

Laplace가 중심극한정리를 발표한 후, 고전주의(오늘날의 Frequentist) 이론가들은 주관적 믿음으로 확률을 인식하는 Bayesian 시각을 오랫동안 반대했습니다. 1800년대(양자 역학이 탄생하기 전)의 많은 과학자들은 자연의 특성(=모수)이 고정되어 있고 관찰/측정에는 오차가 있을 수밖에 없으니 오차의 발생이 무작위적(확률론적)이라고 생각했기 때문입니다. 그러니 자연 상태도 불완전(불확실)함을 전제하는 Bayesian 관점은 고전주의자들에겐 말도 안 되는 생각이었겠죠.

고전주의와 Bayesian은 나름대로 발전하면서 서서히 기틀을 잡아갑니다. 고전주의는 통계학계에서 이미 당연한 주류가 된 상황에서 익숙한 이름의 수학자들이 연구를 거듭하며 지금의 통계학이 되었습니다. 반면, Bayesian은 이론가들이 외면했지만 역사적 사건들 속에서 실무적으로 유용성을 인정받기 시작합니다. 그렇게 인정하기 싫은 쪽과 인정받고 싶은 쪽의 논쟁은 약 200년간 계속됩니다.

 

 

from Classicism to Frequentist

 

 

1. Adophe Quetlet (1796~1874)

통계학의 본질탐구(2) 에서 등장한 이 수학자를 기억하시나요? 벨기에의 천문학자였던 Quetlet는 Laplace에게 확률론을 배웠습니다. 그리고 그의 저서 Sur l'homme et le développement de ses facultés, ou Essai de physique sociale(1835)에서 사회과학에 통계학을 최초로 적용하게 되죠. 물론 정규분포에 적합시켜 주장한 '평균인'이라는 개념과 함께 발생하는 오차에 대해 충분히 설명해내지 못했지만, 그의 연구는 인구총조사(Census)를 시행하는 데에 크게 기여했습니다.

 

 

2. Francis Galton (1822~1911)

19세기와 20세기 통계학의 발전은 '우생학'의 발전과 함께 이루어졌습니다. 우생학(Eugenics)이란 인류의 유전형질을 개량하기 위한 방법을 연구하는 학문으로, 사실 과학적으로 틀린 내용이며 비윤리적으로 활용될 가능성이 많아 지금은 거의 사라진 학문입니다. 이 우생학을 창시한 사람이 바로 Galton입니다. 그의 사촌이 <종의 기원>을 쓴 '찰스 다윈'이었는데, 이 책에 매료된 Galton은 "인간의 능력은 유전되는가?"라는 질문에 답하기 위해 인류의 특성과 변이에 대해 평생동안 연구하게 됩니다. 그래서 그는 많은 데이터를 수집해서 인간의 여러 특성에 대한 척도를 개발해야 했고, 이를 위해 통계적 기술과 설명방법을 반드시 고안해야만 했죠.

 

Quincunx. 출처 :&nbsp;https://jollycontrarian.com/index.php?title=Quincunx

 

Galton은 인구 안정성(Population stability)을 설명하기 위한 수학적 모델을 개발하려고 노력했습니다. 그가 말한 인구 안정성이란 세대를 거치면서도 인간의 특성이 계속 정규분포를 유지하려는 경향을 뜻합니다. 당시 연구로 밝힌 대부분의 요인들은 특성들이 유전되어 정규분포가 유지되는 것이 아니라 각 세대에서 독립적으로 정규분포를 형성함을 뜻하고 있었기에, 부모가 자식에게 끼치는 중대한 영향을 설명하고 싶었던 그에게 정답을 제시해줄 수 없었죠.

 

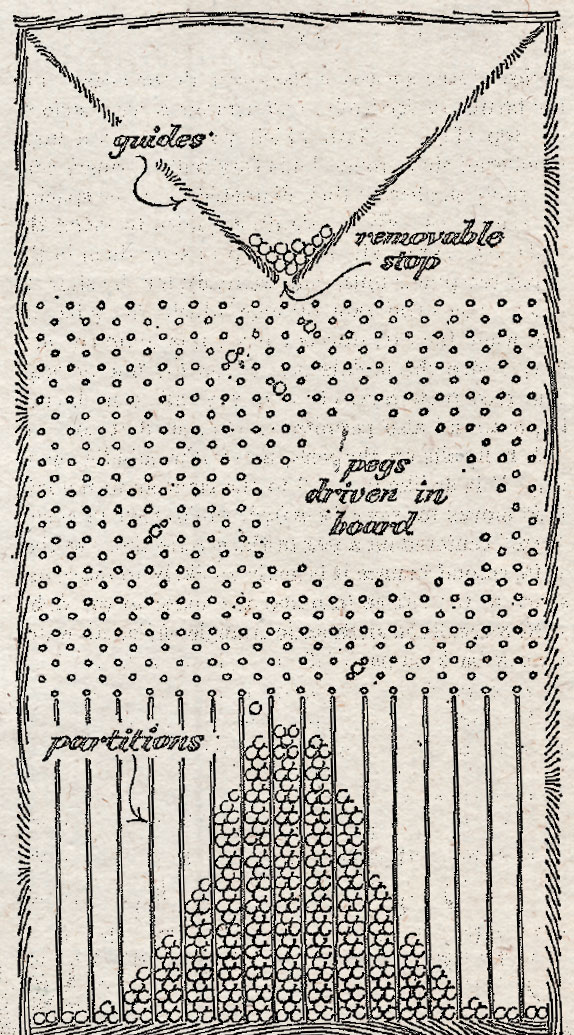
그러다 1877년에 그는 sweet pea(콩과의 식물)을 재배하는 과정에서, 자손 종자들의 무게가 부모 종자들의 무게가 아닌 평균적인 스위트피 종자의 무게(모평균)에 가까운 무게로 집중된다는 것을 발견합니다. 그는 이러한 현상을 역전(recursion, 오늘날  평균으로의 회귀 법칙(law of regression to the mean)과 비슷)이라고 부르고, 위의 그림과 같은 Quincunx라는 장치를 개발하여 이것을 시연해냅니다. 공이 떨어지는 깔때기 부분을 '역전'에 비유하고, 공이 떨어지며 부딪히는 핀들은 '가족 변동성'에 비유해서 정규분포의 특성을 띠며 공들(개체군)(인류)이 쌓이는 것을 자연스러운 현상이라고 밝히게 된 것이죠. 물론 이후 '맨델의 유전법칙' 덕분에 이 아이디어는  유전을 설명하기에 부적절하다는 것이 밝혀졌습니다.

파스칼의 삼각형과 모양새가 비슷하지 않나요? 공이 핀에 부딪혀서 왼쪽 또는 오른쪽으로 떨어질 확률이 서로 같다고 하면, 공이 바닥에 도착할 확률을 구역별로 계산했을 때 그 분포가 종 모양(bell curve)이 됨을 쉽게 알 수 있습니다.

 

** 아래의 사이트에서 Quincunx를 체험해볼 수 있습니다.

Quincunx (Galton Board)

 

출처 :&nbsp;https://en.wikipedia.org/wiki/Regression_toward_the_mean#/media/File:Galton's_correlation_diagram_1875.jpg

 

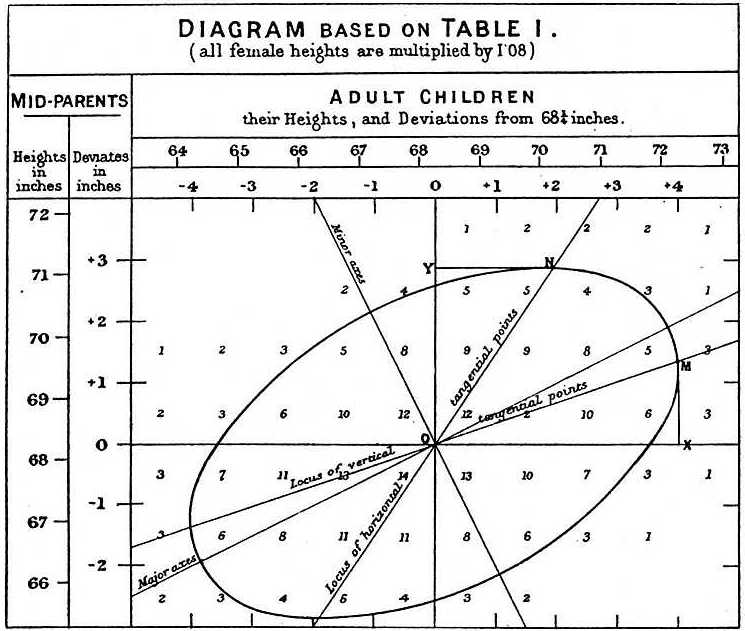
더불어 그는 부모와 자녀의 키 데이터를 분석한 결과, 부모의 극단적인(extreme) 특성이 자녀에게 완전히 전달되지 않으며 오히려 중간 지점(mediocre, 오늘날 '평균')으로 되돌아간다(regress)는 것을 관찰하고 Hereditary Stature(1886)이라는 저서를 발표합니다. 이때 이 저서에서 상관관계(correlation)의 개념을 처음으로 제시하고, 데이터가 어느 축에서든 가운데 중간 지점( \(O\) )을 향하고 있다는 것을 설명하기 위해 위와 같은 삽화를 수록합니다.

향후 평균으로의 회귀 법칙은 여러 실험을 설계할 때 가장 중요한 내용이 되고, Galton의 제자였던 Karl Pearson이 상관계수를 최초로 정의하는 데에 밑거름이 됩니다.

 

 

3. Karl Pearson (1857~1936)

왼쪽이 Karl Pearson, 오른쪽이 Francis Galton. 출처 :&nbsp;https://en.wikipedia.org/wiki/Karl_Pearson#/media/File:Karl_Pearson;_Sir_Francis_Galton.jpg

 

Pearson은 현대의 통계적 가설검정 이론과 통계적 의사결정 이론을 정립한 최초의 인물입니다. 수리통계학 정립에 많은 업적을 남겼고, 1911년에 University College London에 세계 최초의 통계학과를 개설했습니다.

 

그는 Galton의 독실한 제자여서 Galton처럼 우생학을 강력히 지지하는 한편, 생체 인식(Biometrics) 분야의 연구에 몰두해서 생체 측정을 위한 통계적인 기법을 고안하기 위해 노력했다고 하네요. 그 과정에서 Pearson은 그의 논문 On the Criterion That a Given System of Deviations from the Probable in the Case of a Correlated System of Variables Is Such That It Can Be Reasonably Supposed to Have Arisen from Random Sampling(1900)을 통해 p값(p-value)의 개념을 최초로 정의하고 이 값과 경험적 측정값 사이의 카이제곱거리(chi-square distance)를 계산하여 가설의 타당성을 검정해야 한다고 주장합니다.

 

더불어 카이제곱거리 개념으로 범주형(불연속형) 자료의 정규분포 근사를 위한 카이제곱검정(chi-square test)과, 카이제곱거리가 최소가 되도록 다변량 데이터를 선형화하는 주성분분석(PCA, Principal Components Analysis)을 최초로 제시한 사람 역시 Pearson입니다. 히스토그램(histogram)도 그가 최초로 제시한 방법이라고 하네요. 모두 그가 수집한 다양한 생체 데이터를 수리통계학적으로 분석하기 위해 발명해낸 것입니다.

 

 

4. Ronald Fisher (1890~1962)

1900년대 초에는 진화론에서 출발한 우생학 및 생체측정학파(Biometrics, 위의 Galton과 Pearson이 주요 학자였음)와, 우리에게 이른바 '멘델의 유전법칙'을 제시한 Gregor Mendel의 유전학계의 논쟁이 벌어지고 있었습니다. 이때 Ronald Fisher도 우생학을 열렬히 지지했지만, 멘델의 유전법칙이 카이제곱검정으로 완벽하게 검증되는 것을 발견한 그는 이 논쟁을 해결하기 위해 오랫동안 연구했다고 합니다. 그리고 The Genetical Theory of Natural Selection(1930)이라는 저서를 출간하면서 다윈의 진화론과 멘델의 유전학을 종합하여 현대 진화이론(Modern Synthesis)을 정립하는 데에 기틀을 제시합니다.

 

1932년판. 출처 : https://openlibrary.org/books/OL17638309M/Statistical_methods_for_research_workers

 

그리고 Fisher는 오늘날 통계분석에 있어 가장 영향을 많이 끼친 Statistical Methods for Research Workers(1925)를 출간합니다. 이 책은 다양한 분석방법을 활용한 후 종합적으로 결론을 도출하는 '메타분석(Meta-Analysis)'을 해내기 위한 지침서로 활용되었다고 합니다. 이 책의 수많은 업적 중 하나는 바로 통계적 유의성의 한계를 최초로 제시했다는 것입니다. 그는 우연적으로 예상을 벗어날 확률이 1/20을 넘으면 통계적으로 무의미하다고 주장했는데, 이것이 (정규분포에서) 오늘날 유의수준을 \(\alpha=0.05\)로 두고 p값이 유의수준보다 작을 때 귀무가설을 기각한다는 가설검정의 체계가 됩니다. p값이 0.05일 때(신뢰수준이 95%일 때) 표준정규분포에서 약 1.96에 위치한다는 내용도 이 책에서 등장한 것이랍니다. 원문은 아래와 같습니다.

(p46) The value for which P = 0.05, or 1 in 20, is 1.96 or nearly 2 ; it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not.

 

더불어 3개 이상의 집단을 비교할 때 F-분포를 활용하는 분산분석(ANOVA), 두 개 이상의 군집을 구분하는 기준을 찾아내는 선형판별분석(LDA, Linear Discriminant Analysis)을 발명하고 유명한 데이터셋인 'Iris(붓꽃)'데이터를 함께 제시합니다. 오늘날 통계적 추론에서 반드시 필요한 최대우도추정법(MLE, Maximum Likelihood Estimation)의 개념 역시 그가 발명해냅니다. 1998년에 덴마크의 통계학자인 Anders Hald는 통계학 역사책을 집필하면서, Fisher에 대해 "현대통계학의 멱살을 혼자 잡고 발전을 이끈 천재(a genius who almost single-handedly created the foundations for modern statistical science)"라고 평가하기도 했다네요.

 

 

5. Jerzy Neyman (1894~1981)

폴란드의 수학자 Jerzy Neyman은 Frequentist probability and frequentist statistics(1977) 이라는 논문에서 우리가 알고 있는 'Frequentist'라는 이름을 처음 쓰기 시작했습니다. Neyman이 지금까지 불리던 '고전주의(classicism)'라는 용어를 Frequentist(빈도주의)로 대체한 이유에 대해, 미국의 통계학자 Bradley Efron(Bootstrap 방법을 발명한 사람)은 '표준의(canonical)', '기본적인(foundational)' 등의 뜻으로 읽힐 수 있는 '고전적(classical)'이라는 단어보다 더 중립적(neutral)이면서도 Bayesian과 비교했을 때 더 본질적인 느낌을 전달하고 싶어했을 것으로 추측합니다(Efron and Hastie, 2016).

 

Jerzy Neyman. 출처 :&nbsp;https://en.wikipedia.org/wiki/Jerzy_Neyman#/media/File:Jerzy_Neyman2.jpg

 

그는 Frequentist라는 단어를 만들어냈을 뿐만 아니라, 가설 검정에서 활용하는 신뢰구간(Confidential Interval)의 개념을 최초로 제시합니다. 또한 위의 Karl Pearson의 아들인 Egon Pearson(1895~1980)과 함께 가설검정에서의 제1종 오류(실제(귀무가설)로 참인데 거짓이라고 판단하는 경우)와 제2종 오류(실제(귀무가설)로 거짓인데 참이라고 판단하는 경우)의 개념을 정립하고, 최강력검정(Most Powerful Test)에 관한 보조 정리인 'Neyman-Pearson Lemma'를 만들어내는 등 많은 업적을 남겼습니다.

 

 

 

Bayesian의 발전

 

 

위에서 살펴본, 각종 이론과 교재에 셀 수 없이 등장하는 이름의 통계학자들은 모두 Bayesian에 강력하게 반대했고 우생학을 지지하며 연구했던 사람들입니다. Bayesian이라는 용어도 1950년에 Fisher가 '그들'을 지칭하면서 등장한 용어죠. 또한 이들 모두 University College London의 우생학과 학과장을 역임한 사람들입니다.

그러나 제2차 세계대전(1939~1945)을 겪으면서 우생학이 많은 비난을 받기 시작했고, 한편으로 Bayesian 방법이 조용히 발전했습니다. 전범국인 나치 독일의 철학이 우생학에 기반한 것이었기 때문이죠. 또 전쟁의 승리를 예측하거나 이끌어내는 데에 Bayesian 방법이 효과적이라는 것이 증명되면서 본격적으로 주목을 받았기 때문입니다.

 

 

1. Alan Turing (1912~1954)

Enigma(May 1937).

 

영국의 수학자 Alan Turing은 제2차 세계대전 시기에 독일 해군의 암호기계 'Enigma'를 해독한 수학자입니다. 2014년 영화 <이미테이션 게임>으로 대중들에게 많이 알려지기도 한 Turing은 Enigma를 해독하는 기계 'Bombe Machine'을 만들 때, 암호화된 알파벳의 실제 알파벳이 무엇일지 가능성을 평가하는 도구로서 베이즈 정리를 활용합니다. 아주 간단하게 원리를 살펴볼까요?

 

Enigma는 어떤 알파벳을 기계 하부 키보드에 타자로 입력하면 무작위 알파벳으로 변환하여 기계 상부에 있는 그 알파벳의 자리에 불이 들어오도록 하는, 일종의 함수같은 기계입니다. 아래와 같은 그림의 구조를 갖고 있는데, a를 입력하면 f가 나오고, b를 입력하면 d가 나오고, c를 입력하면 e가 나오는 것이죠. 이때 '쌍'을 이루고 있기 때문에 그 반대도 성립(self-inverse)합니다. f를 입력하면 a가 나오고, d를 입력하면 b가 나오고, e를 입력하면 c가 나옵니다. 그래서 당시 독일 해군의 통신원이 Enigma로 메시지를 암호화하여 라디오 주파수를 통해 읽어보내면, 수신원이 다시 Enigma에 암호화된 알파벳을 입력하여 해독된 메시지를 이해하는 구조였다고 하네요.

 

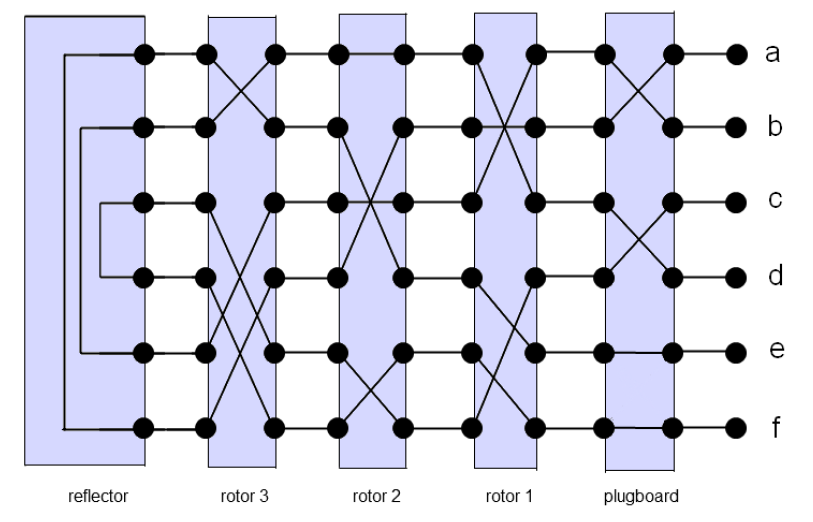
그런데 문제는 이 '알파벳 대응쌍'이 매일 바뀌었다는 것입니다. 그러니 독일군의 주파수를 도청을 해도 해독하는 데에 너무 오래걸리고(26개의 알파벳으로 가능한 경우의 수를 모두 따져야 함) 그걸 매일 다시 해야했으니, 전쟁에서 열세에 있었던 연합군은 골치가 아팠을 겁니다. 폴란드의 수학자들이 암호를 풀기 위한 시도도 있었으나, 해독하고 있다는 정보를 독일군이 입수하면서 결국 실패하고 말았죠. 그런데 이것을 Turing은 혼자서 해결해냅니다! 독일군이 암호 해독의 시도를 알지 못하도록 외부에 알리지 않은 것이죠.

 

먼저 Turing과 그의 조수들은 일상적으로 사용하는 언어 속에서 통계적으로 자주 등장하는 알파벳 덩어리를 정리한 표인 'bigram table'을 활용하여 독일군이 전송하는 메시지의 시작과 끝에 달린 'message indicator'(알파벳 3개가 한 묶음, ex. KQK)가 있음을 발견합니다. 그리고 이 message indicator가 당일 해독의 기준이 된다는 것도 알아내죠. 예를 들어 시작부분에 KQK가 있고 끝부분에 IVS가 있으면, 그날은 KQK라고 이름붙인 알파벳 서열(chain)과 IVS라고 이름붙인 알파벳 서열이 하나의 쌍이 된다는 뜻입니다.

 

그런데 정보를 수집하던 이들은 message indicator의 첫 두 글자가 같으면, indicator가 뜻하는 알파벳 서열도 비슷하다는 것을 발견합니다. 예를 들어 KQK와 KQB의 서열이 비슷하다는 것이죠. 그래서 이들은 두 서열 중 한 서열을 3개씩 이동(shift)시켰을 때 알파벳이 일치하는 경우를 'in depth'라고 불렀습니다. 예를 들어 이렇습니다.

D, W, W, E, Y, R, Q가 in depth인 상황입니다.

 

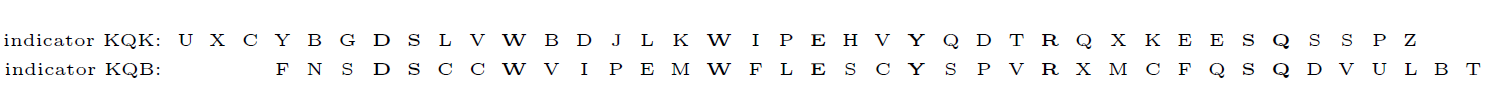
일반적으로 알파벳이 무작위로 등장할 확률은 \(\frac{1}{26}\)이지만, 실제로 영어에서는 \(\frac{1}{15}\)이고 독일어에서는 \(\frac{1}{17}\)이라고 합니다. 그래서 Turing은 암호화된 알파벳과 실제 알파벳이 같을 확률을 계산하고 원래 서열(chain)을 추적합니다. 이때 베이즈 정리를 활용하는데, 정답인 알파벳을 우리가 알아낼 확률을 아래와 같이 계산합니다.

 

(1)

원래 베이즈 정리를 이렇게도 쓸 수 있습니다. \(A_1\)과 \(A_2\), \(B\)는 어떤 사건을 뜻합니다.

 

$$P(A_1\mid B)=\frac{P(B\mid A_1)}{P(B)}\cdot P(A_1)$$

$$P(A_2\mid B)=\frac{P(B\mid A_2)}{P(B)}\cdot P(A_2)$$

$$\therefore \frac{P(A_1\mid B)}{P(A_2\mid B)}=\frac{P(B\mid A_1)}{P(B\mid A_2)}\cdot \frac{P(A_1)}{P(A_2)}$$

 

(2)

이때 \(A_2\)가 \(A_1\)의 여사건(complement)이면, 사건\(A_1\)의 Odds(발생하지 않을 확률 대비 발생할 확률)를 $O(A_1)$라 둘 때 이렇게 다시 쓸 수 있습니다.

 

$$O(A_1\mid B)=\frac{P(B\mid A_1)}{P(B\mid {A_1}^c)}\cdot O(A_1) $$

 

(3)

이때 in depth가 발생할 확률이 바로 \(O(A_1)\)이 됩니다. 알파벳이 다들 일치하지 않을 확률 대비 알파벳이 일치할 확률이니까요. 그리고 사건 \(B\)가 실제 메시지의 알파벳인 사건(match)으로 두면, 아래와 같이 대입해볼 수 있습니다.

 

$$O(in\;depth \mid match)=\frac{P(match \mid in\;depth)}{P(match \mid not\;in\;depth)}\cdot O(in\;depth)$$

$$= \frac{1/17}{1/26}\cdot O(in\;depth)$$

$$= \frac{26}{17}\cdot O(in\;depth)$$

 

$$O(in\;depth \mid nonmatch)=\frac{P(nonmatch \mid in\;depth)}{P(nonmatch \mid not\;in\;depth)}\cdot O(in\;depth)$$

$$= \frac{1-(1/17)}{1-(1/26)}\cdot O(in\;depth)$$

$$= \frac{416}{425}\cdot O(in\;depth)$$

 

이때 \(\frac{26}{17}\)과 \(\frac{416}{425}\)이 각각 알파벳을 적중시켰을 때와 적중시키지 못했을 때 그 서열(chain)의 유용성(오늘날의 Bayesian Factor(BF, 베이즈 인자))이 됩니다. 그래서 이 숫자를 알파벳별로 조합하여 구한 'composite bayesian factor'를 서열 후보군마다 구해서 가장 값이 높은 서열이 실제 알파벳일 가능성이 높은 서열이 됩니다.

 

Bombe Machine.

 

이렇게 가능한 모든 경우의 수에 대한 확률 및 composite bayesian factor를 구해주는 기계가 바로 위의 그림과 같은 Bombe Machine입니다. 이후 독일군은 Enigma 암호를 쓰다가 이보다 더 어려운 Lorenz 암호를 쓰기 시작했는데, 이 또한 연합국의 학자들이 위와 비슷한 원리로 해독해냅니다. 이렇게 암호를 해독해낸 것은 실제로 제2차 세계대전을 연합군이 승리하는 데에 많이 기여했다고 하네요. 하지만 당시 영국 총리 윈스턴 처칠은 영국이 암호를 해독해낼 수 있다는 사실을 소련은 모르게 하기 위해 관련된 모든 문서를 파기하라고 지시했고, 1973년이 되어서야 Alan Turing이라는 수학자의 존재와 Bayesian의 장점이 세상에 드러나게 됩니다.

 

 

2. Jerome Cornfield (1912~1979) 

출처 :&nbsp;https://americanhistory.si.edu/blog/2014/03/smoke-gets-in-your-eyes-20th-century-tobacco-advertisements.html

 

1950년대 후반에 "담배는 흡연을 유발하는가?"에 대한 논쟁이 강렬했다고 합니다. 1902년에 미국의 담배 시장에서 궐련형 담배가 차지하는 비율은 2%에 불과했지만, 공장에서 대량생산이 가능해지고 위와 같이 담배를 긍정적으로 홍보하는 광고가 많아지면서 1952년이 되자 궐련형 담배는 담배 시장에서 무려 81%를 차지합니다. 흡연자가 기하급수적으로 늘면서 정부와 보건 당국도 담배에 주목하고, 이 당시에 폐암 환자 또한 급속도로 증가하면서 흡연과 폐암 간의 어떤 상관관계가 있는 것이 아닌가 의심하게 됩니다.

 

이때 Richard Doll과 Austin B. Hill이라는 학자가 폐암 환자들과 건강한 사람들을 인터뷰하는 식으로 흡연과 폐암 간의 상관관계에 대한 연구를 진행했습니다. 그러나 이 연구에는 실험군과 대조군이 명확하지 않다는 문제가 있었기에, 결국 이들은 방법을 바꿔서 6만명의 영국 의사에게 흡연 습관에 대한 설문지를 배포하고 이들을 5년간 관찰하는 'prospective study'를 진행했습니다. 결과적으로 흡연자가 비흡연자보다 폐암으로 사망할 확률이 24배 높다는 것을 밝혀냅니다.

그러나 당시 저명한 학자였던 (위에서도 언급한) Ronald Fisher는 이 연구가 사람의 체질, 습관 등 '교란변수'를 고려하지 않았으므로 잘못된 연구였다고 주장합니다. Doll과 Hill은 그렇다고 실험군에게 담배를 피우도록 하는 실험을 할 수도 없었고, 영향력있는 학자의 위세가 있었기에 Fisher에 대응할 수 없었죠.

 

이때 Fisher의 주장에 정면으로 반박한 사람이 바로 Jerome Cornfield입니다. 그는 사람이 갖고 있는 '흡연 유전자'(체질)라는 것이 있다면 모든 흡연자에게 그 유전자가 발견이 되어야 할 텐데, 절대 그렇지 않다고 주장합니다. 즉, '유전자의 차이로 인해 사람이 흡연을 한다'는, 말은 되지만 현실적으로 규명하기 어려운 것을 상관관계에서 고려해서는 안 된다는 것이죠.

 

Jerome Cornfield. 출처 : https://biostatcenter.gwu.edu/people/directors/jerome-cornfield

 

Cornfield의 주장은 Bayesian 방법이 의학계에서 활용되기 위한 철학적 기초를 제공합니다. 그는 현실 세계에서 수집된 수많은 데이터에만 의존하는 고전적인 방법(오늘날의 Frequentist)은 위와 같이 논리적인 난제를 초래하고 융통성이 없을 수 있음을 지적하고, 가능성과 믿음을 정량화하고 업데이트하는 Bayesian 방법을 함께 활용해야 한다고 주장했습니다.

 

 

3. Markov Chain Monte Carlo (MCMC)

20세기 후반에 들어 이전에 비해 Bayesian 방법에 대한 인식은 많이 개선되었지만, 여전히 과학적 연구에 '주관'이 들어간다는 특성 때문에 현실적으로 객관성을 얻기 어려웠습니다. 또한 베이즈 정리를 이용해서 수치를 계산해야 하는데, 손으로 복잡한 숫자의 분수를 계산하는 것이 매우 어려웠죠. 그런데 컴퓨터가 발명되면서 'Random Sampler(난수 생성기)'를 편리하게 사용할 수 있게 되자 판도가 완전히 바뀌어버립니다. 

 

제2차 세계대전 당시 미국이 주도했던 핵무기 개발계획인 '맨해튼 계획(Manhattan Project)'을 아시나요? 이 계획에 당시 수학자 John von Neumann(1903~1957)과 Stanislaw Ulam(1909~1984)이 참여하고 있었습니다. 이때 Ulam이 한번은 급성 뇌염이 와서 수술을 받고 회복하고 있었는데, 회복 도중 핵분열성 물질의 중성자 확산을 성공적으로 해낼 확률을 계산하기 위해 당시 세계 최초의 컴퓨터였던 애니악(ENIAC)으로 수백 번의 시도를 해보면 어떨까 하는 아이디어를 떠올렸다고 합니다!

 

John von Neumann. 출처 :&nbsp;https://www.cantorsparadise.com/the-unparalleled-genius-of-john-von-neumann-791bb9f42a2d

Stanislaw Ulam. 출처 :&nbsp;https://en.wikipedia.org/wiki/Stanislaw_Ulam#/media/File:Stanislaw_Ulam.tif

Nicholas Metropolis. 출처 :&nbsp;http://photoarchive.lib.uchicago.edu/db.xqy?one=apf1-11737.xml

 

이 아이디어를 들은 같은 연구실(Los Almos laboratory)의 수학자 Nicholas Metropolis(1915~1999)는 Ulam과 함께 논문 The Monte Carlo Method(1949)을 발표합니다. 이 방법은 데이터를 수집하여 하나의 예측 모델을 만들어내던 기존의 방식과 달리, 관심이 있지만 불확실한 확률변수에 대해 확률분포를 주관적으로 지정하고 표본의 범위를 임의로 판단하여 반복적으로 확률변수의 표본들을 무작위로 생성(시뮬레이션)해내는 방식입니다. 예측 모델을 구축하기에 충분히 많은 표본이 생성되었다고 판단될 때 생성을 멈추는 것이죠.

이름이 조금 특이한데, '몬테카를로'는 프랑스 밑에 있는 모나코라는 작은 국가에 있는 한 카지노의 이름입니다. Ulam의 삼촌이었던 Michal Ulam이 자꾸 도박을 하러 몬테카를로에 가야한다고 얘기하는 바람에 Metropolis가 영감을 얻어 이렇게 이름을 지었다는 이야기도 있고, 계속 표본을 생성하는 과정이 도박을 하는 것과 비슷하여 당시 유명한 카지노 이름인 몬테 카를로를 차용했다는 이야기도 있습니다.

Ulam과 Metropolis의 1949년 논문 첫 페이지. 출처 :&nbsp;https://www.jstor.org/stable/2280232

 

특히 1909년에 러시아의 수학자 Markov(1856~1922, 러시아어: Андре́й Андре́евич Ма́рков)가 제시했던 'Markov Chain(마르코프 연쇄)' 개념을 혼합한 Markov Chain Monte Carlo(MCMC) 라는 방법은 Bayesian 연구에 엄청난 기여를 하게 됩니다. Markov Chain이란 이산적으로 줄지어 발생하는 확률변수들 각각의 조건부 확률분포가 바로 직전의 확률변수(직전의 상태)에만 영향을 받아 결정된다는 개념(확률과정의 일종)입니다. 간단히 예를 들어 확률변수 $X_1$, $X_2$, $X_3$ 이 세 사건이 차례로 발생하는 Markov chain이 있다고 하면, $X_3$의 확률분포는 바로 직전의 상태인 $X_2$에게만 영향을 받아 생성될 뿐 $X_1$로부터 영향을 받지 않는다는 뜻이죠.

이 MCMC라는 시뮬레이션 방법은 직접 관찰한 많은 데이터에만 의존하지 않고, 먼저 연구자의 주관에 따라 관심이 있는 어떤 변수의 확률분포(=사전분포)를 정한 후 시뮬레이션을 해나가면서 자신의 주관(믿음, 판단)을 갱신한다는 점에서 Bayesian 방법을 컴퓨터로 실현할 무한한 가능성을 제공해주었습니다. 

 

 

정리 및 결론

 

 

초기의 과학자들은 Bayes의 아이디어가 말도 안 되는 이야기라고 생각했지만, 시간이 흘러 쓰임을 인정받으면서 살아남은 Bayesian 통계학은 이제 Frequentist와 대등한 위치로 자리매김했습니다. 특히 머신러닝과 인공지능이 급속도로 발달하면서 미래를 예측하는데 유용한 Bayesian 방법은 더욱 주목받고 있습니다. 그러나 여전히 주류는 Frequentist입니다. 대학에서 개설되는 대부분의 전통적인 통계학 과목들이 빈도주의를 기반으로 한 과목들인 것만으로도 알 수 있죠.

앞으로 우리는 Cornfield의 주장과 같이, 통계학의 두 분야가 서로의 대체재가 아닌 보완재가 되고 있다고 생각하는 것이 좋겠습니다. 데이터 수집에 한계가 있어 유의미한 추론이 어려울 때 Bayesian Framework를 사용하여 추론의 범위를 넓히고, 실험 전 최초의 믿음/판단(=사전분포)을 결정하는 데에 있어 기존의 확률분포 또는 데이터를 적절히 활용하는 것은 이미 통계학계에서 널리 사용되고 있는 연구방법일 것입니다. 학생의 입장에서는 공부량이 2배로 늘어난 것이니 고통스러울 수도 있겠군요!

 

 

요약 및 용어정리

 

	Frequentist(빈도주의)
확률에 대한 인식	개연성 = 객관적(장기적) 빈도 = 확률
모수(\(\theta\))에 대한 인식	고정된 상수(숫자. 하나의 자연상태)
실험 방법	추정 : 점추정 또는 구간추정 검정 : 귀무가설이 참이라고 가정하고 실험 시작 -> 수용/기각 여부 결정(연역적) - 불확실성을 줄이려고 노력

 

	Bayesian(베이지안)
확률에 대한 인식	개연성 = (주관적) 믿음 = 확률
모수(\(\theta\))에 대한 인식	확률변수(불확실한 개체)
실험 방법	주관적 믿음이 있는데, 가능성/증거 수집으로 믿음을 갱신(귀납적) - 불확실성을 인정 및 전제 \(\therefore\) 귀무가설(사전분포)과 대립가설(사후분포) 각각에 대한 믿음의 정도를 계산(Bayes factor)하고 믿음이 몇 배 증가했는지 계산

 

Reference

 

Cornfield J et al. (2009) Smoking and lung cancer: recent evidence and a discussion of some questions. JNCI 1959; 22:173–203. Reprinted with permission.

James Grime. (2019). Math from the Talk: "Alan Turing and Enigma Machine."

Metropolis, N., & Ulam, S. (1949). The Monte Carlo Method. Journal of the American Statistical Association, 44(247), 335–341. https://doi.org/10.2307/2280232

Pearson, K. (1900) On the Criterion That a Given System of Deviations from the Probable in the Case of a Correlated System of Variables Is Such That It Can Be Reasonably Supposed to Have Arisen from Random Sampling. Philosophical Magazine Series 5, 50, 157-175. http://dx.doi.org/10.1080/14786440009463897

 

Smoke gets in your eyes: 20th century tobacco advertisements

A History of Bayes' Theorem - LessWrong

베이즈 통계(1): 서론

Monte Carlo Simulation: History, How it Works, and 4 Key Steps

What is Monte Carlo Simulation? | IBM